주요 도구 : 드레인 전류식, KVL
1. MOSFET Bias
증가형, NMOS를 기준으로 설명한다.
1.1 전압분배 Bias


게이트 전압은 위의 식처럼 R1,R2의 분배로 공급된다.
1.1.1 포화영역에서 동작을 해야되고, 그렇다면 아래식을 만족한다.
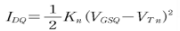
1.1.2 그리고 포화영역 동작조건.

; Vds가 유효게이트 전압보다 커야, 채널형성후 Pinch-off효과로 VDS의 영향을 제거할 수 있다.
1.1.3 Drain ~ source에 KVL
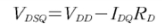
1.1.4 위식을 토대로 부하선(Load line) 방정식을 구하면

1.1.5 위의 부하선을 그래프에 표시하면

위와 같은 결과를 얻을 수 있다.
동작점(Q점)
부하선(파란직선)과 교점, VGS를 알고 있어야 결정된다.
1.1.6 천이점(transition point)
; MOSFET포화 영역의 경계(Vds=Vgs-Vtn) 포물선과 부하선의 교점
1.2 포화영역에 있기 위한 게이트 전압의 최대값


VDS
VDS는 위의 식으로 표현된다. ID를 대입하면

VDS식에 ID대입
유효게이트 전압이 관찰포인트이다. 이것은 0보다 크므로, 유효게이트전압(VGS-Vtn)에 대해 식을 정리하면
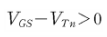

>0 이므로, 근호 앞이 (-)은 해는 제거된다.
Source = GND(0[V]) 에 연결되있으므로 VGS = VG이다. 따라서,
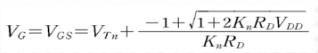
이 값은 포화영역에 있을 때, VGS의 값이다.
아래 예제를 통해서 다시 정리하는 것이 더 깔끔할 것 같다.
1.3 예제

1. VGS

= (20 / 40+20 )(12) = 4V
2. ID
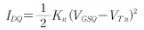
= 1/2*(0.4)*(10E-3)*(4-2)^2 = 0.8[mA]
3. VDS

4. 포화영역

VDS가 유효게이트전압(2V)보다 높아서 포화영역 Bias임이 확인됨.
=> VGS는 전압분배, ID는 공식, VDS는 KVL로 구하고
포화영역 확인으로 DC해석을 마무리했다.

그래프를 통해 예제 결과 확인

1.3의 예제 시뮬레이션 결과
1.3.1 위 예제의 심화문제
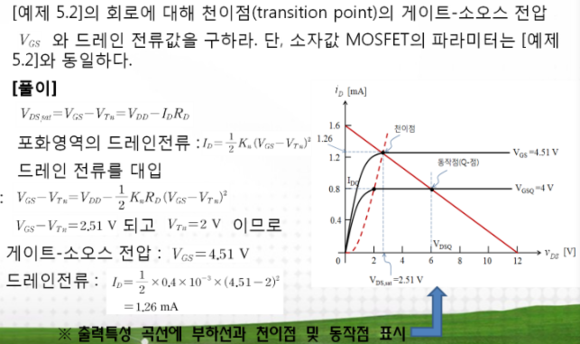
1.3.1.1 천이점 : 포화영역 경계에 놓여있다.
1.3.1.2 이때, VDS = VGS-Vtn이고, KVL을 적용하면 VDD-IDRD이다.
1.3.1.3 여기에 ID값을 대입하는데, 이것을 VGS-VTn에 대해 정리하여 구하면 VGS = 2.51[V]의 결과를 얻을 수 있다.
1.3.1.4 VTn = 2[V]이므로, VGS = 4.51[V] , ID = 1.26[mA]
1.4 예제2

1.4.1 Kn이 없으므로 Kn먼저 주어진 상수를 이용해 구한다.
1.4.2 포화영역 가정
1.4.3 Drain전류 구하기(공식)
1.4.4 VDS구하기(KVL)
1.4.5 포화영역 확인 VDS>VGS-VTn
2.1
자기바이어스(Self-bias)
위의 전압분배 + source저항(RS)의 형태이다.
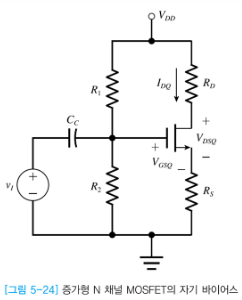
전압분배 + RS
2.2
DC해석 방법은 위에서 한것 처럼
-> 전압분배, ID, KVL, 포화영역 확인을 이용해 구한다.

2.3 자기바이어스 부하선, 동작점 그래프
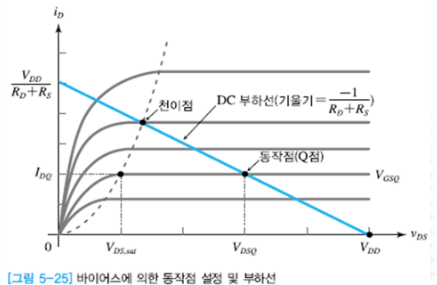
동작점 : 부하선과 특성곡선이 만나는점
천이점 : 부하선과 경계선(포화/비포화)이 만나는점
2.4 예제1

2.4.1. RS, RD, R1+R2저항값 구하기
-> 기본적인 소자의 값이 정해져 있지 않으므로, 저항값을 구한다.
바이어스 저항(R1,R2,RD,RS)에 흐르는 전류가 50uA이므로,
옴의 법칙을 이용
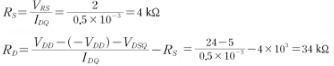
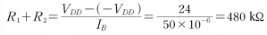
2.4.2. VGS,VG구하고 이를 통해 R1,R2를 구해보자.
ID는 주어졌으므로, ID공식을 이용해 VGS를 구한다.

VGS를 통해 VG를 구한다.

VG는 R1,R2의 전압분배로, 이 관계를 이용하면 R1,R2를 VG와 연관지을 수 있다.

위에서 구한 R1+R2와, 위의 식을 연립하면 R1= 382k, R2= 98k를 구할 수 있다.
2.4.3. 시뮬레이션 결과
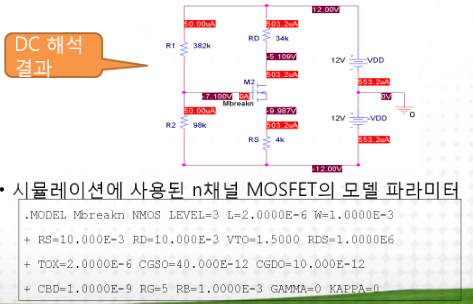
3. 공핍형 MOFET바이어스
; VGS가 (+), (-) 모두 가능하다.
3.1
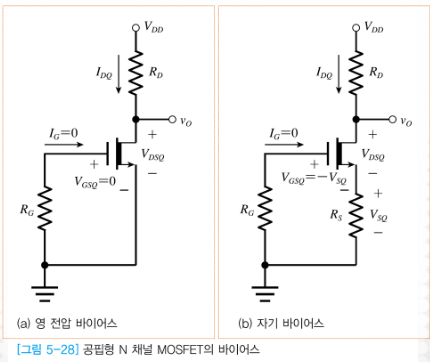
3.1(a) 영전압 바이어스
VGS =0, 포화영역 일 때, 드레인 바이어스 전류.

드레인 바이이어스 전류
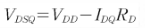
드레인 바이어스 전압
3.1(b) 자기 바이어스
Vg = 0을 걸고, Rs를 통해 Vs를 걸어 주다.

Rs를 통해 VS라는 일정한 (-)전압이 걸린다.
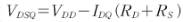
드레인 바이어스 전압은 KVL적용
3.2 예제
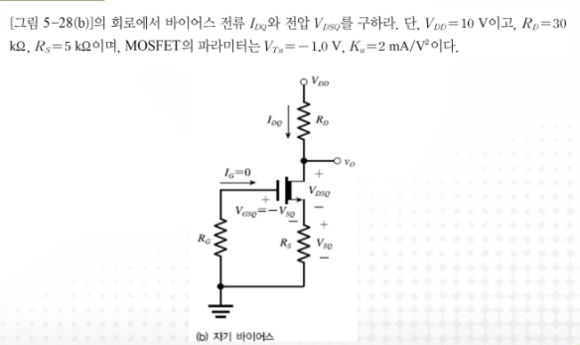
1. 심볼을 보면 공핍형인 것을 알 수 있다.
2. Rs로 Vs의 자기바이어스를 걸어 줬다.
3. Drain bias 전류

위 식을 풀면 Id = 0.13 or 0.31 mA
조건을 찾아보자.
Drain 전류의 최대값은 Vds =0일 때, 흐른다.
[IDQ = (VDD -VDS)(RS+RD)]

이 값보다 작아야 하므로, Id = 0.13mA
4. Drain~source bias 전압
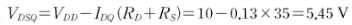
출처 : KOCW. 전자회로. 영남대학교. 김성원
http://contents.kocw.or.kr/contents4/html/2013/Yeungnam/KimSungwon/11-1/default.htm
'전공지식정리 > 전자회로' 카테고리의 다른 글
| 연산증폭기(OP Amp) 1. 개요 (0) | 2020.12.07 |
|---|---|
| FET4(JFET의 DC해석, FET의 AC해석) (0) | 2020.12.07 |
| FET2(MOSFET I-V특성, JFET구조) (0) | 2020.12.07 |
| FET1(MOSFET구조, 동작) (0) | 2020.12.07 |
| BJT증폭기 5(증폭기 비교, 설계 예제) (0) | 2020.12.07 |